[Stat] What is "BLUE"

BLUE = Best Linear Unbiased Estimator
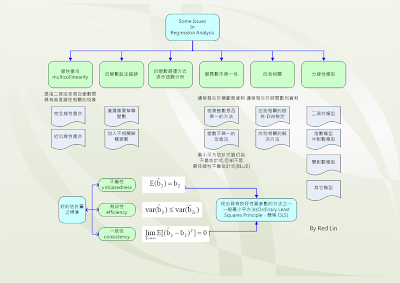
在簡單線性迴歸中，根據高斯-馬可夫定理 (Gauss-Markov Theorem)
只要殘差符合以下的假設，我們使用一般最小平方法來估計Beta時，
就可以得到具有~最佳線性不偏估計量(BLUE)的性質.

迴歸模型的殘差 (residual) 必需符合以下的性質 (古典迴歸的假設)
1. 殘差期望值為零 (zero mean) : E(u) = 0
2. 殘差具同質變異 (homoskedasticity) : var(u) = σ^2，σ^2為constant
3. 殘差無自我相關 (non-autocorrelation) : cov(ut, ut-s) = 0, for s ≠0
4. 自變數與殘差無相關 (orthogonality) : cov(x, u) = 0, for any i
* 文獻上亦將符合以上要求之殘差稱為獨立相同分配(iid)殘差
5. 殘差為常態性 (normality)
* 如果簡單線性迴歸殘差亦符合以上第 (5) 個假設，則 OLS 所得到之估計式也將具有常態分配的性質，不過只要樣本數夠大，OLS 所得到估計式之分配將可漸進為常態分配。所以其重要性在樣本數多的時候就相對較不重要。

使用 OLS 估計時BLUE 性質的重要性:
殘差若不符合高斯-馬可夫定理的要求，則我們用 OLS 所估得之係數，就不一定會具有 BLUE 的性質。根據沒有BLUE 性質的迴歸係數進行統計決策或推論，在實務應用上會有較高的錯誤機率。

所以正確的步驟應該為:
使用 OLS 進行估計時，應該先檢查殘差是否符合高斯-馬可夫定理對迴歸殘差的假設要求，通過符合假設之檢定後，再對迴歸係數進行統計推論才是正確的迴歸分析步驟。

*殘差具同質變異 (homoskedasticity)及自變數與殘差無相關(orthogonality) (假設(2)及假設(4))
a. 變異數不同質之原因，來自殘差與自變數相關，又可稱為比例異質性 (proportional heteroskedasticity) –常用White’s test
b. 變異數不同質之原因，來自變異數和殘差落後期平方相關，又稱為自我相關異質變異 (Autoregressive Conditional Heterorscedasticity, ARCH) –常用ARCH-LM 檢定及Q 平方檢定
*殘差無自我相關 (non-autocorrelation) (假設(3))
殘差間是否存在自我相關的性質 –常用Q 檢定進行檢定
*殘差之期望值是否為零 (zero mean) (假設(1))
由於使用OLS 估計之殘差大多很接近

[R] Distribution Probability

Some function can use in (Normal, T, Uniform, F, Chi-Squared...Distribution)
ex: Normal distribution,
dnorm(x, mean = 0, sd = 1, log = FALSE)
pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
rnorm(n, mean = 0, sd = 1)
#p <- quantiles, and gives probabilities
pnorm(c(1.645,1.96,3.1))
>[1] 0.9500151 0.9750021 0.9990324

#q <- probabilities, and gives quantiles
qnorm(c(0.95,0.975,0.999))
>[1] 1.644854 1.959964 3.090232

#d <- number, and gives the density
x<-seq(-3,3,0.01)
plot(c(1:length(x)),dnorm(x))
#r <- generates random deviates
x<-rnorm(1000)
mean(x) # ~0
sd(x) # ~1

Nice Graph- explain simple regression estimate

Show the true regression line and the random error term
ε is assumed to follow the normal distribution with
a mean of 0 and variance of σ square

Scientist: Four golden lessons

1. I must start doing research, and pick up what I needed to know as I went along.

2. Go for the messes — that's where the action is.
3. Forgive yourself for wasting time.
4. Learn something about the history of science, or at a minimum the history of your own branch of science.
Ref: http://www.nature.com/nature/journal/v426/n6965/full/426389a.html